《2.1 代数式》基础训练
1. 下列式子符合代数式的书写格式的是.
A．
B. 
C. 
D. 
2. 下列说法正确的是.
A．单项式
既没系数，也没次数
B. 单项式
的系数是5
C. －2006也是单项式
D. 
的系数是－3
3. 下列说法中，正确的是.
A. 4＝3x是代数式 B. 6是代数式
C. a不是代数式 D. 
不是代数式
4. 三个连续偶数，假如中间的数是2n，那样较小的偶数是.
A. 2n－1 B. 2 C. n－2 D. 2
5. 下列关于
的次数说法正确的是.
A. 2次 B. 3次 C. 0次 D. 没办法确定
6. 
，x＋1，－2，
，0.72xy，各式中单项式的个数是.
A. 2个 B.3个 C.4个 D.5个
7.单项式的系数、次数分别是.
A. 0，2 B. 0， 4 C. －1，5 D. 1，4
8.下列说法中，正确的是.
A．－7
的系数是7 B．－
的系数是－1
C．－
的次数是7 D．－
的次数是5
9. 下列式子中不是代数式的是.
A．x＋y B．0 C．
D．m＞0
10. 下列代数式中，符合书写规范的个数有.
①－2x；②m÷5；③1.5x；④
n；⑤x－2米．
A．2个 B．3个 C．4个 D．5个
11. 假如
为四次单项式，则m＝_______.
12. 
是______次______项式，其中三次项系数是______，二次项为______，常数项为______，写出所有些项____________.
13. “a与b的差的平方的c倍”用代数式表示为___________.
14. 某产品的原价是100元，假如经过两次降价且降价的百分率都是x，那样该产品目前的价格是__________元.
15. 当
，
时，求下列代数式的值：
； 
.
答案和分析
【答案】
1. B 2. C 3. B 4. B 5. C
6. C 7. C 8. B 9. D 10. A
11. 4 12. 三 三 －1 
1
13. 
14. 
15.
；
.
【分析】
1. 解：应写成
，故选项A错误；
应写成
，故选项C错误；
应写成
，故选项D错误.
故选B.
代数式的书写规范：
在代数式中，假如出现乘号，可写成“
”或不写.数字与字母相乘时，为省略乘号，数字写在字母前. 字母与字母相乘时，相同字母写成幂的形式. 数字与数字相乘时，“×”号不可以省；
假如式中出现除法，一般写成分数形式.
2. 解：单项式的系数是1，次数也是1，故选项A错误；
单项式的系数是，故选项B错误；
单独的一个数或一个字母也是单项式，故－2006也是单项式，选项C正确；
的系数是，故选项D错误；
故选C.
由数与字母的乘积组成的代数式叫做单项式.单独的一个数或一个字母也是单项式.单项式中的数字因数叫做这个单项式的系数.一个单项式中，所有字母的指数之和叫做这个单项式的次数.
3. 解：4＝3x是方程，不是代数式，故选项A错误；
单个的数或字母也是代数式，则6是代数式，故选项B正确；
单个的数或字母也是代数式，则a是代数式，故选项C错误；
是代数式，故选项D错误.
故选B.
像如此用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子，就叫做代数式.单个的数或字母也是代数式.
4. 解：三个连续偶数，假如中间的数是2n，那样较小的偶数是2n－2，即2，
故选B.
相连偶数相差2，假如中间的数是2n，那样较小的偶数是2n－2.
列代数式时要弄了解题中的数目关系，运算顺序，书写代数式时要规范.
5. 解：中不含字母，所以次数不是1，而是0，
故选C.
一个单项式中，所有字母的指数之和叫做这个单项式的次数.不含字母的单项式的次数是0.
6. 解：依据单项式的概念可知，x＋1，－2，，0.72xy都是单项式，
故单项式的个数是4个.
故选C.
由数与字母的乘积组成的代数式叫做单项式.单独的一个数或一个字母也是单项式.
7. 解：单项式的系数是－1，次数是2＋1＋2＝5，
故选C.
一个单项式中，所有字母的指数之和叫做这个单项式的次数.注意单项式的次数是所有字母的指数和，不可以加上系数中的指数.
8. 解：－7的系数是－7，故选项A错误；
－的系数是－1，故选项B正确；
单项式的次数是所有字母的指数和，不可以加上系数中的指数，－的次数是2＋3＝5，故选项C错误；
－的次数是1＋3＋2＝6，故选项D错误.
故选B.
单项式中的数字因数叫做这个单项式的系数.一个单项式中，所有字母的指数之和叫做这个单项式的次数. 单项式的次数是所有字母的指数和，不可以加上系数中的指数.
9. 解：依据代数式的概念可知，x＋y，0，是代数式，m＞0不是代数式，
故选D.
像如此用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子，就叫做代数式.单个的数或字母也是代数式.
10. 解：代数式中，符合书写规范的有－2x，1.5x，故符合书写规范的个数是2，
m÷5应写成
，n应写成，x－2米应写成米，
故选A.
代数式的书写规范：
在代数式中，假如出现乘号，可写成“”或不写.数字与字母相乘时，为省略乘号，数字写在字母前. 字母与字母相乘时，相同字母写成幂的形式. 数字与数字相乘时，“×”号不可以省；
假如式中出现除法，一般写成分数形式.
11. 解：假如为四次单项式，则1＋m－1＝m＝4，
故答案为4.
一个单项式中，所有字母的指数之和叫做这个单项式的次数.
12. 解： 是三次三项式，其中三次项的系数是－1，二次项为，常数项为1.
故答案为三，三，－1，，1.
在多项式中，每一个单项式叫做多项式的项，多项式的每一项都包含它前面的符号.其中不含字母的项，叫做常数项. 一个多项式含有几项，这个多项式就叫做几项式.一个多项式里，次数最高的项的次数，叫做这个多项式的次数.
13. 解：“a与b的差的平方的c倍”用代数式表示为，
故答案为.
列代数式时要弄了解题中的数目关系，运算顺序，书写代数式时要规范.
14. 解：某产品的原价是100元，降价的百分率是x，则降价后的价格是
，
若经过两次降价且降价的百分率都是x，那样该产品目前的价格是元.
列代数式时要弄了解题中的数目关系，运算顺序，书写代数式时要规范.
15. 解：当，时，
求代数式的值的步骤：代入，即用数值代替代数式里的字母；计算，即根据代数式指明的运算顺序，计算出结果.
《2.1 代数式》提升训练
1. 下列各式：①2x－1；②3；③c＝2
r；④＋1＞0；⑤st；⑥
.其中是代数式的有个．
A. 2个 B.3个 C.4个 D.5个
2. 用代数式表示“x的4倍与y的差的平方”，正确的是.
A． B．
C．
D．
3. 代数式
用语言叙述正确的是.
A．a与4b的平方差 B．a的平方减4乘以b的平方
C．a的平方与b的平方的4倍的差 D．a与4b差的平方
4. 若x是2的相反数，|y|＝3，则x－y的值是.
A．－5 B．1 C．－1或5 D．1或－5
5. 如图，两个正方形的面积分别为16，9，两阴影部分的面积分别为a，b，则等于.
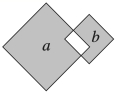
A．7 B．6 C．5 D．4
6. 已知代数式的值是8，那样代数式
的值是.
A．1 B．2 C．3 D．4
7. 已知代数式
，则代数式的值是.
A．15 B．17 C．－15 D．－17
8. 某企业今年3月份产值是a万元，4月份比3月份降低了10%，5月份比4月份增加了15%，则5月份的产值是_________万元.
9. 某市出租车的起步价是5元，超越3千米的每千米按1.4元计费，则某人乘出租车行x（x>3且x为整数）千米应对费是________元.
10. 若|x－1|＋|y＋3|＝0，则的值是________．
11. 含盐15%的盐水200 g，在其中加入m g盐后，盐水含盐百分率是.
A. B. 
C. D.
12. 已知代数式的值是8，那样代数式的值是.
A．1 B．2 C．3 D．4
13. 在修建电影院时，为了获得最好的观看成效，第一排设计a个座位，后面每排比前一排多2个座位．
试用式子表示第n排的座位数；
若此电影院设计座位为20排，试用式子表示最后一排的座位数；
在条件下，若最后一排座位数为60个，请你设计第一排的座位数．
答案和分析
【答案】
1. C 2. A 3. C 4. D 5. A 6. D 7. B
8. 
9. 1.4x＋0.8 10. 20 11. D 12. B
13. a＋2 n－2； a＋38；22.
【分析】
1. 解：结合数轴可知，－1＜a ＜0，b＞1，|a|＜1＜|b|，所以a＋b＞0，
依据代数式的概念可知：①2x－1；②3；⑤st；⑥是代数式，共4个，
故选C.
像如此用加、减、乘、除及乘方等运算符号把数或表示数的字母连接而成的式子，就叫做代数式.单个的数或字母也是代数式.
2. 解：依据题意，可列代数式为，
故选A.
列代数式时要弄了解题中的数目关系，运算顺序，书写代数式时要规范.
3. 解：代数式用语言叙述为a的平方与b的平方的4倍的差，
故选C.
在用语言描述代数式时，应该注意运算顺序的描述，容易出错.
4. 解：∵x是2的相反数，
∴x＝－2，
又∵|y|＝3，
∴y＝3或－3，
∴x－y＝－2－3＝－5或x－y＝－2－＝1，
即x－y的值是1或－5.
故选D.
本题考查的是代数式求值，依据相反数和绝对值的概念可知，x＝－2，y＝3或－3，进而可以求出x－y的值.
5. 解：结合图形可知，设空白部分的面积是c，
故a＝16－c，b＝9－c，
故a－b＝16－c－＝7，
故选A.
此题考查的是代数式求值的应用，依据题意，弄了解题中的数目关系，列出代数式，进行计算即可. 设空白部分的面积是c，结合图形可知，a＝16－c，b＝9－c，进而可以求出a－b的值.
6. 解：－11－3＝－11＋＝－14（℃），最大温差为14℃；
－11－＝－11＋＝－8（℃），最大温差为8℃；
3－＝3＋＝6（℃），最大温差为8℃；
所以，任意两城市中最大的温差是14℃.
故选D.
依据题意，分别求出任意两城市的温差，进而得出任意两城市中最大的温差即可.
此题考查的是有理数减法的应用，对于这种题要依据题意列出算式，进而求出结果．
7. 解：已知代数式，
则代数式，
故选B.
本题考查的是代数式求值，在解题过程中，察看代数式的特征，将已知条件进行变形直接代入需要的代数式，可以更容易求出代数式的值.
8. 解：3月份产值是a万元，4月份比3月份降低了10%，
则4月份的产值是，
若5月份比4月份增加了15%，
则5月份的产值是.
故答案为.
依据题意，弄了解题中的数目关系，列出代数式，进行化简即可.
9. 解：因为x>3，即某人乘出租车所行超越3千米，所付成本分为两部分：
起步价5元； 超越3千米的每千米按1.4元计费，则超越部分的成本为1.4元；
故某人乘出租车行x（x>3且x为整数）千米应对费是
1.4＋5＝1.4x－4.2＋5＝1.4x＋0.8.
故答案为1.4x＋0.8.
依据题意，弄了解题中的数目关系，列出代数式，进行化简即可.解题重点是明确所付成本分为两部分：起步价5元； 超越3千米的每千米按1.4元计费，则超越部分的成本为1.4元.
10. 解：依据绝对值的非负性可得，x－1＝0，y＋3＝0，
则x＝1，y＝－3，
.
故的值是20.
故答案为20.
此题考查的是代数式求值，依据绝对值的非负性，由|x－1|＋|y＋3|＝0可得，x－1＝0，y＋3＝0，求出x、y的值，进而可以求出代数式的值.
11. 解：含盐15%的盐水200 g，在其中加入m g盐后，盐的水平为15%×200＋m＝30＋m，盐水的水平为200＋m，
故盐水含盐百分率是，
故选D.
依据题意，弄了解题中的数目关系，列出代数式，进行化简即可.解题重点是明确盐水含盐百分率是用盐的水平比上盐水的水平. 加入m g盐后，盐的水平为15%×200＋m，盐水的水平为.
12. 解：已知代数式的值是8，即
，
可得，
，
那样，，
则，
即代数式的值是2.
故选B.
本题考查的是代数式求值，在解题过程中，察看代数式的特征，将已知条件进行变形直接代入需要的代数式，可以更容易求出代数式的值.
此题考查的是代数式求值，对于输入取不一样的值x，最后的输出结果不同.
13. 解：解：已知第一排设计a个座位，后面每排比前一排多2个座位，
则第n排比第一排多2个座位，
所以，第n排的座位数为a＋2＝a＋2 n－2；
当n＝20时，最后一排的座位数为a＋2 n－2＝a＋2×20－2＝a＋38；
若最后一排座位数为60个，则a＋38＝60，
所以，a＝22.
剖析出第n排比第一排多2个座位，则可以求出第n排的座位数；将n＝20代入代数式即可；由可知，a＋38＝60，求出a的值即可.
此题考查的是代数式求值的应用，依据题意，弄了解题中的数目关系，列出代数式，进行计算即可.
